Tag Archives: WiMAX

Qualcomm In Muddy Waters In India

September 25, 2011Network Planning, Random ThoughtsCalifornia, India, LTE, Qualcomm, WiMAXYasir Ahmed (aka John)

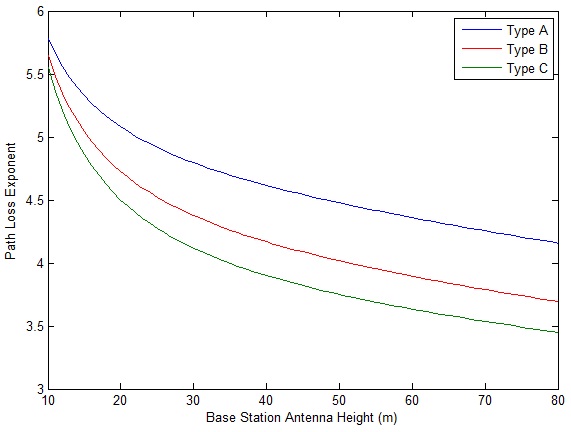
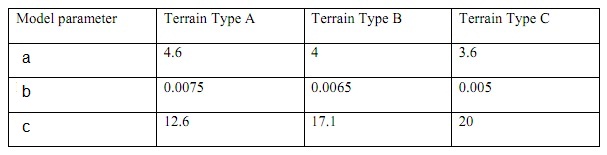
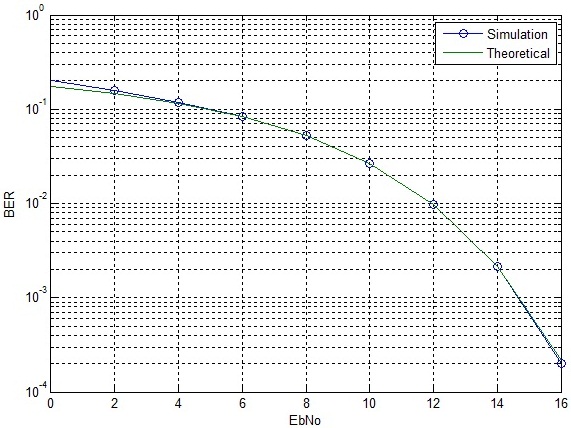
Remember Qualcomm CEO Paul Jacobs proudly claiming that his company had prevented WiMAX from getting a hold in India by acquiring BWA licenses in four regions of India. Well now Qualcomm is in a bit of bother as the Department of Telecommunication (DoT) in India has raised objections to the license application filed by Qualcomm. According to news circulating on the internet the DoT has objected to Qualcomm filing four separate applications through its nominee companies in the four regions (Delhi, Mumbai, Kerala and Haryana) it had won the licenses on June 12, 2010. Secondly the DoT has also objected to the delay in the filing of application outside the three month period required by the laws.

Qualcomm has rejected these objections saying that it has followed all rules in letter and spirit. According to Qualcomm the license application was filed in August 2010 within the three month period as required by the laws. However this is disputable as Qualcomm also submitted a revised application in December 2010. Qualcomm has also countered the second objection by saying that it plans to merge the four nominee companies so that there is no breach of law. As per the rules “if at any stage the spectrum allocation is revoked, withdrawn, varied or surrendered, no refund will be made”. So if an understanding is not reached between Qualcomm and DoT, Qualcomm is set to lose more than $1 billion that it had paid for the BWA spectrum.

Qualcomm Inc. is a leading wireless chip manufacturing company of the world. It is the pioneer of CDMA technology and its chipsets have been embedded in more than a billion cell phones. Qualcomm has greatly invested in UMTS technology and is a strong proponent of WCMDA, HSPA and LTE standards. It had a paid about a billion dollars for the right to use a 20 MHz chunk of spectrum in the 2.3 GHz band. It plans to bring TDD LTE to India, which is a considered to be a comparatively economical 4G technology.

WiMAX Path Loss and Antenna Height

September 24, 2011Network Planning, WiMAXAntenna, Network Planning, Path Loss, WiMAXYasir Ahmed (aka John)

As discussed previously the SUI (Stanford University Interim) model can be used to calculate the path loss of a WiMAX link. The SUI model is given as:

: SUI Path Loss Equation

It has five components:

1. The free space path loss (A) up to the reference distance of ‘do’.
2. Additional path loss for distance ‘d’ with path loss exponent ‘n’.
3. Additional path loss (Xf) for frequencies above 2000 MHz.
4. Path gain (Xh) for receive antenna heights greater than 2 m.
5. Shadowing factor (s).

The most important factor in this equation is the distance dependent path loss. The impact of this factor is controlled by the path loss exponent ‘n’. It is well known that in free space the path loss exponent has a value of 2. In more realistic channels its value ranges anywhere from 2 to 6. For SUI model the path loss exponent is calculated as:

n=a-(b*hb)+(c./hb)

where a, b and c are SUI model specific parameters. It is obvious that the path loss exponent decreases with increase in base station antenna height ‘hb’. The path loss exponent for various antenna heights is shown below.

: Path Loss Exponent

It is observed that as the base station antenna height is varied from 10 m to 80 m the path loss exponent for the three scenarios varies from around 5.5-6.0 to 3.5-4.5. Basically what this means is that for higher base station antenna heights the cell radius would be larger. However we need to be careful when making this statement. Higher antenna heights also sometimes results in a weak signal area close to the base station. This is where the antenna downward tilt becomes an important factor. Antenna downward tilt usually has a value around 5-10 degrees. It is somewhat surprising that although it is such an important factor none of the well known empirical models take it into account.

Note: SUI Model was initially formulated based upon the data collected by AT&T Wireless across the United States in 95 existing macrocells at 1.9 GHz.

WiMAX Path Loss Calculation

September 23, 2011Channel Modeling, WiMAXNetwork Planning, Path Loss, WiMAXYasir Ahmed (aka John)

Calculation of the path loss is fundamental to Wireless System Design. There are many models available for calculating the path loss such as Okumura Model, Hata Model, COST-231 Model and more recently the SUI (Stanford University Interim) Model. The SUI Model has been specifically proposed for Broadband Wireless Access Systems such as WiMAX. It defines three types of environments namely A, B and C which are equivalent to the urban, suburban and rural environments defined in the earlier models. According to this model the path loss can be calculated as:

PL=A+10*n*log10(d/do)+Xf+Xh+s

where

n=a-(b*hb)+(c/hb)
A=20*log10(4*pi*do/lambda)
Xf=6.0*log10(f/2000)
Xh=-10.8*log10(hr/2) for A&B
Xh=-20.0*log10(hr/2) for C

and

frequency of operation = f = >2000MHz
transmit receive separation = d = 100 m to 8000 m
reference distance = do = 100 m
base station antenna height = hb = 10 m to 80 m
receive antenna height = h = 2 m to 10 m
shadowing factor with lognormal distribution = s = 8.2 dB to 10.6 dB

The values for the parameters a,b and c for the three environment are given in the table below.

Doing a quick calculation for f=2500 MHz, hb=30 m, hr=2 m, s=8.2, do=100 m and d=1000 m gives us a path loss 137.13 dB for Type-A channel. Increasing the frequency to 3500 MHz (another WiMAX band) increases the path loss to 140.93 dB i.e. there is a 3.8 dB increase in the path loss.

So to recap the path loss given by the SUI model is composed of 5 elements:

Bit Error Rate of 64-QAM in AWGN

September 1, 20115G, BER Performance, LTE, Modulation, WiMAXBER, LTE, WiMAXYasir Ahmed (aka John)

64-QAM is an important modulation scheme being used in WiMAX and LTE. It allows for transmission of 6 bits symbol which results in higher bit rate and spectral efficiency. The calculation of bit error rate of 64-QAM is a bit tricky as there are many different formulas available with varying degrees of accuracy. Here, we first calculate the bit error rate (BER) of 64-QAM using a simulation and then compare it to the theoretical curve for 64-QAM.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO CALCULATE 64-QAM BER USING SIMULATION
% n_bits: Input, number of bits
% EbNodB: Input, energy per bit to noise PSD
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= M_QAM(n_bits,EbNodB);
M=64;
k=log2(M)
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
n=randn(1,n_bits/k)+j*randn(1,n_bits/k);
y=y+sqrt(7/(2*EbNo))*n.';
h2=modem.qamdemod(M)
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,y);
ber=(n_bits-sum(x==z))/n_bits
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% CALCULATE 64-QAM BER USING FORMULA
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
EbNodB=0:2:16;
EbNo=10.^(EbNodB/10);
k=6;
M=64;
x=sqrt(3*k*EbNo/(M-1));
Pb=(4/k)*(1-1/sqrt(M))*(1/2)*erfc(x/sqrt(2));
semilogy(EbNodB,Pb)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Using the above functions the BER of 64-QAM is calculated as shown below. Also shown is the constellation diagram of 64-QAM after addition of noise.

It is observed that the theoretical curve almost overlaps the simulation results. There is only a very small difference at very low signal to noise ratio. The BER of 64-QAM at 16dB is approximately equal to the BER for QPSK at 8dB. Therefore the 64-QAM can only be used in scenarios where there is a very good signal to noise ratio.

In this post we have used built in MATLAB functions for modulation and demodulation. In future posts we try to build up the simulation without using these functions!