Near Field of an Antenna

The Electromagnetic Radiation from an antenna, particularly dipole antenna, has been studied in great detail. The mathematical framework proposed by Maxwell has stood the test of time and theoretical concepts have been verified through physical measurements. But the behavior of Electromagnetic (EM) waves close to the radiating antenna is not that well understood. This region that extends to about a wavelength from the antenna is called Near Field, as opposed to Far Field, which extends further out. The Near Field is further divided into Reactive Near Field and Radiative Near Field.

We know that in the Far Field the E-field, H-field and directional of propagation are all perpendicular to each other and E-field and H-field are in phase. The impedance of free space (given as ratio of E-field and H-field) in this region is equal to 377 ohms (120π ohms). But this is not the case in Near Field where E-field is much greater than H-field and these fields are not in phase. Furthermore the rate of decay of E-field and H-field is much higher in the Near Field.

Given below is the code that plots the E-field and H-field (normalized, so that rate of decay can be compared) in the three regions. It can be seen that there is no clear boundary defining the three regions; the fields and resulting impedance gradually change as the distance from the transmit antenna increases. In the far field both the E-field and H-field decay at 10dB/decade. In the region closest to the antenna E-field decays at 30dB/decade whereas H-field decays as 20dB decade.  

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
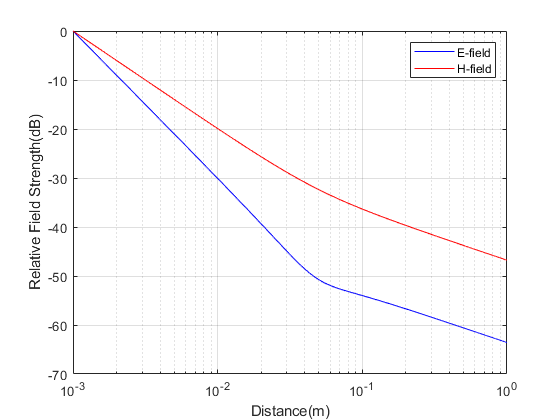
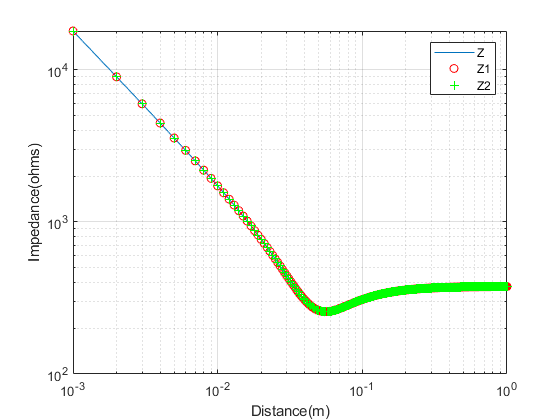
% E-field and H-field of a Small Dipole Antenna
% f is the frequency
% c is the speed of light
% lambda is the wavelength
% k is the wave number
% L is the length of the antenna
% nue is the characteristic impedance of free space
%
% Copyright www.raymaps.com (2022)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all

f=1e9;
c=3e8;
lambda=c/f;
k=2*pi/lambda;
L=lambda/10;
nue=377;
Io=1;
theta=pi/2;

r=0.001:0.001:1;

E_theta=i*nue*k*Io*L*sin(theta)./(4*pi*r).*(1+1./(i*k*r)+1./(i*k*r).^2).*exp(-i*k*r);
semilogx(r,10*log10(abs(E_theta)/max(abs(E_theta))),'b');hold on

H_phi=i*k*Io*L./(4*pi*r).*(1+1./(i*k*r))*sin(theta).*exp(-i*k*r);
semilogx(r,10*log10(abs(H_phi)/max(abs(H_phi))),'r');hold off
xlabel('Distance(m)')
ylabel('Relative Field Strength(dB)')
legend('E-field','H-field')
grid on

Z=E_theta./H_phi;
figure;loglog(r,abs(Z));hold on

Z1=nue*(1+1./(i*k*r)+1./(i*k*r).^2)./(1+1./(i*k*r));
loglog(r,abs(Z1),'ro');hold on

Z2=nue*(1-1./(k^2*r.^2-i*k*r));
loglog(r,abs(Z2),'g+');hold off
xlabel('Distance(m)')
ylabel('Impedance(ohms)')
legend('Z','Z1','Z2')
grid on
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Note:

1. Please note that we have used the E-field and H-field equations derived for a small dipole and kept the length of the dipole to be one tenth of the wavelength.

2. We have used three methods to plot the impedance; from definition of impedance (Z=E/H), from the formula for impedance (Z1) and simplified formula for impedance (Z2).

3. The exact formula for calculating the length of Near Field is given as NF=2*(D^2)/l, where l is the wavelength and D is the length of the antenna.  But this formula is only valid for large antennas.     

Reference:

https://nptel.ac.in/content/storage2/courses/108101092/Week-2-Dipole%20Antenna.pdf 

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin