As previously discussed, finding the frequency of a complex sinusoid embedded in noise is a classical problem in Signal Processing. The problem is compounded by the fact that number of samples available is usually quite small. So far, we have discussed Zero Crossing, FFT, MUSIC and ESPRIT methods of frequency estimation. Zero Crossing method is simplest of the above four but it can detect only one sinusoid at a time. Advantage of Zero Crossing method is that it is computationally not that complex. It does not require complex matrix manipulations as some of the other methods do.

Now we present another single frequency estimator that is quite easy to implement. It is known as Kay’s Estimator [1] after its founder Steven M. Kay.  Although quite simple to implement it achieves Cramer Rao Lower Bound (CRLB) for moderate to high SNRs (SNR>10dB). The basic concept of Kay’s estimator is quite simple. It finds the phase advanced from one sample to the next and this gives us the frequency. Averaging is performed over the time window to get more accurate results. Averaging can be performed using uniform weighting or a weighting function defined by Kay in [1]. In the latter case CRLB is achieved with equality, so there is no need to look for another estimator.

Mathematically CRLB is given as:

Mean Squared Error (MSE) in Angular Frequency=6/(SNR*N*(N^2-1))

Where N is the number of samples (set to 100 in this case) and SNR is the Signal to Noise Ratio (set to 10dB). MATLAB/Octave code for both the methods (with different weighting functions) is given below. For the example given CRLB is calculated as:

MSE=6/(10*100*(100^2-1))=-62.22dB

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%  FREQUENCY ESTIMATION USING
%      KAY's ESTIMATOR
%   (SINGLE FREQUENCY ONLY)
%      www.raymaps.com
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
close all

N=100;
fc=1.0e9;
fs=20*fc;
w=2*pi*fc/fs;

n=0:N-1;
s=sqrt(1.0)*exp(i*w*n);
wn=sqrt(0.1/2)*(randn(1,N)+i*randn(1,N));
x=s+wn;

% KAY ESTIMATOR-1 (uniform weighting)
w_est=0;
M=N;
for m=1:M-1
  w_est=w_est+(1/(M-1))*arg((x(m))'*x(m+1));
end
error_1=w-w_est;

% KAY ESTIMATOR-2 (using weighting function)
w_est=0;
M=N;
for m=1:M-1
  p(m)=6*(m)*(M-m)/(M*(M^2-1));
  w_est=w_est+p(m)*arg((x(m))'*x(m+1));
end
error_2=w-w_est;

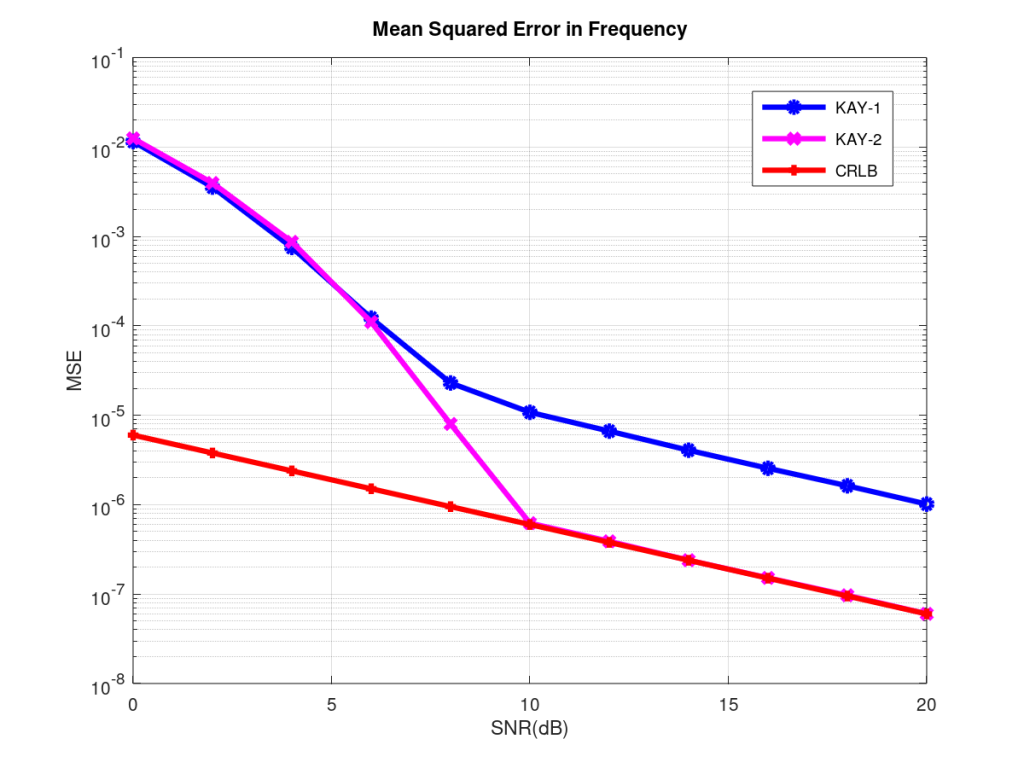
Note:

1. If you want the complete code for comparing the MSE of the two methods with CRLB please leave a comment below and I will get back with you.
2. Please note that as the number of samples N is increased the CRLB and Mean Squared Error (MSE) both go down. But after a time the law of diminishing returns sets in and MSE does not go down as rapidly as the CRLB.
3. The MSE also depends upon number of samples per cycle and having a very small number does not help in reducing the MSE. A few complete cycles work the best (in our code we use five complete cycles to do the estimation).

Reference:

[1] S. M. Kay, “A Fast and Accurate Single Frequency Estimator,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 37, no. 12, Dec 1989.

Author: Yasir Ahmed (aka John)

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked as a Research Assistant within the Mobile and Portable Radio Group (MPRG) of Virginia Tech and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. The collaboration with MPRG continued even after graduating with an MSEE degree and has resulted in 12 research publications and a book on Wireless Communications. Worked for Qualcomm USA as an Engineer with the key role of performance and conformance testing of UMTS modems. Qualcomm is the inventor of CDMA technology and owns patents critical to the 4G and 5G standards.

Twitter Facebook Linkedin