BER of 64-QAM OFDM in AWGN

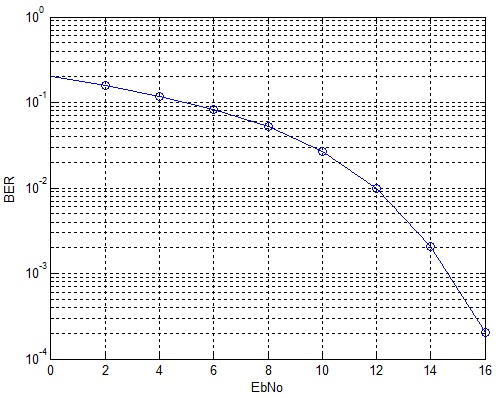
64-QAM is an important component of the LTE Air Interface that promises higher data rates and spectral efficiencies. Combined with OFDM and MIMO it successfully combats the detrimental effects of the wireless channels and provides data rates in excess of 100Mbps (peak data rate). Here, we discuss a simple example of 64-QAM modulation with OFDM in an AWGN channel. We assume a bandwidth of 1.25MHz which corresponds to an FFT size of 128.

Given below is the code for this scheme.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO CALCULATE BER OF 64-QAM OFDM IN AWGN
% n_bits: Input, number of bits
% n_fft: Input, FFT size 
% EbNodB: Input, energy per bit to noise PSD
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= M_QAM(n_bits,n_fft,EbNodB);
Eb=7;
M=64;
k=log2(M);
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
n_sym=length(y)/n_fft;
s_ofdm=zeros(1,n_fft);
r_ofdm=zeros(1,n_fft);
for n=1:n_sym;
s_ofdm=sqrt(n_fft)*ifft(y((n-1)*n_fft+1:n*n_fft),n_fft);
wn=randn(1,n_fft)+j*randn(1,n_fft);
r_ofdm=s_ofdm+sqrt(Eb/(2*EbNo))*wn.';
s_est((n-1)*n_fft+1:n*n_fft)=fft(r_ofdm,n_fft)/sqrt(n_fft);
end
h2=modem.qamdemod(M);
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,s_est.');
ber=(n_bits-sum(x==z))/n_bits;
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

As discussed previously, with proper normalization of IFFT and FFT operations the performance of OFDM in AWGN is the same as the performance of the underlying modulation scheme. We have not even introduced the cyclic prefix in our simulation because without a fading channel there is no ISI and cyclic prefix (CP) is of no use. We will introduce the CP when we turn our attention to fading channels.

It must be noted that although IFFT and FFT are linear inverses of each other proper normalization is required to maintain the signal levels at the transmitter and receiver.

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin