Bit Error Rate of 64-QAM in AWGN

64-QAM is an important modulation scheme being used in WiMAX and LTE. It allows for transmission of 6 bits symbol which results in higher bit rate and spectral efficiency. The calculation of bit error rate of 64-QAM is a bit tricky as there are many different formulas available with varying degrees of accuracy. Here, we first calculate the bit error rate (BER) of 64-QAM using a simulation and then compare it to the theoretical curve for 64-QAM.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO CALCULATE 64-QAM BER USING SIMULATION
% n_bits: Input, number of bits
% EbNodB: Input, energy per bit to noise PSD
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= M_QAM(n_bits,EbNodB);
M=64;
k=log2(M)
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
n=randn(1,n_bits/k)+j*randn(1,n_bits/k);
y=y+sqrt(7/(2*EbNo))*n.';
h2=modem.qamdemod(M)
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,y);
ber=(n_bits-sum(x==z))/n_bits
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% CALCULATE 64-QAM BER USING FORMULA
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
EbNodB=0:2:16;
EbNo=10.^(EbNodB/10);
k=6;
M=64;
x=sqrt(3*k*EbNo/(M-1));
Pb=(4/k)*(1-1/sqrt(M))*(1/2)*erfc(x/sqrt(2));
semilogy(EbNodB,Pb)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Using the above functions the BER of 64-QAM is calculated as shown below. Also shown is the constellation diagram of 64-QAM after addition of noise.

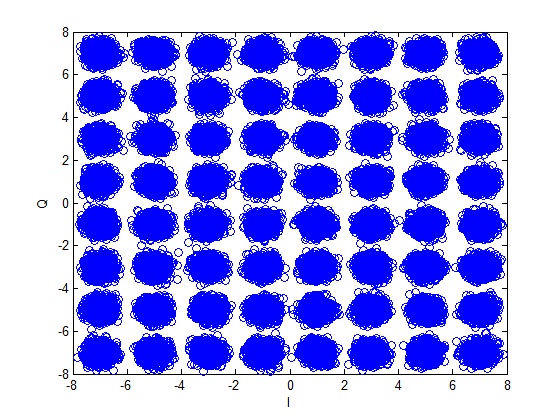
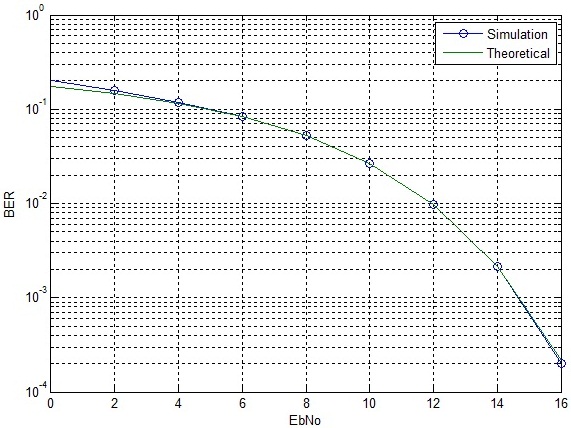
It is observed that the theoretical curve almost overlaps the simulation results. There is only a very small difference at very low signal to noise ratio. The BER of 64-QAM at 16dB is approximately equal to the BER for QPSK at 8dB. Therefore the 64-QAM can only be used in scenarios where there is a very good signal to noise ratio.

In this post we have used built in MATLAB functions for modulation and demodulation. In future posts we try to build up the simulation without using these functions!

Author: Yasir

More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.

Twitter Facebook Linkedin