So we have seen that multiple transmit antennas provide the same gain as multiple receive antennas if the channel state information can be fed back to the transmitter. But what if the channel state information cannot be fed back to the transmitter (or it can be done but not quickly enough). The solution to this problem is the so called “Alamouti Scheme”. In this scheme two symbols are simultaneously transmitted from two transmit antennas and in the next time slot phase shifted versions of these two symbols are transmitted over the two transmit antennas. The channel is assumed to be quasi static i.e. it is static over the duration of two time slots but then changes for the next two time slots. A combining scheme is used at the receiver which separates the two symbols.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% l: Length of symbol sequence
% EbNo: Energy per bit to noise power spectral density
% ber: Output bit error rate
% Copyright www.raymaps.com
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]=err_rate7(l,EbNo)
s1i=2*(round(rand(1,l))-0.5);
s1q=2*(round(rand(1,l))-0.5);
s1=s1i+j*s1q;
s2i=2*(round(rand(1,l))-0.5);
s2q=2*(round(rand(1,l))-0.5);
s2=s2i+j*s2q;
n1=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
n2=(1/sqrt(2*10^(EbNo/10)))*(randn(1,l)+j*randn(1,l));
h1=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
h2=(1/sqrt(2))*((randn(1,l))+j*(randn(1,l)));
r1=h1.*(sqrt(1/2)*s1)+h2.*(sqrt(1/2)*s2)+n1;
r2=-h1.*conj(sqrt(1/2)*s2)+h2.*conj(sqrt(1/2)*s1)+n2;
s1_=conj(h1).*r1+h2.*conj(r2);
s2_=conj(h2).*r1-h1.*conj(r2);
s1i_=sign(real(s1_));
s1q_=sign(imag(s1_));
ber1=(l-sum(s1i==s1i_))/l;
ber2=(l-sum(s1q==s1q_))/l;
ber=mean([ber1 ber2]);
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
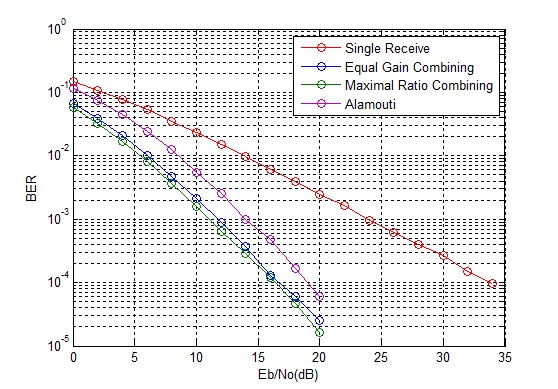
It is observed that this scheme is 3dB worse than MRC (and transmit diversity with CSI). This reason for this is that unlike MRC the signals are transmitted from two transmit antennas thus the power is halved at each transmit antenna (this scheme is also 3dB worse than transmit diversity with CSI at transmitter because although both schemes transmit half the power from each source but in this scheme the noise power is doubled due to the combining scheme working over two time slots).
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
One thought on “Alamouti Scheme”
Raj: What this expression is doing is essentially introducing a phase shift before the transmission such that after passing through the channel the signal has zero phase shift. The expression (conj(h1)./abs(h1)) introduces the phase shift at the Tx and multiplication at the Rx in the expression h1.*sr1 cancels that phase shift. Note we only adjusted the phase and not the amplitude. Hope this makes sense!