In the previous post we had considered a static frequency-selective channel. We now consider a time-varying frequency selective channel with 7 taps. Each tap of the time domain filter has a Gaussian distributed real component with variance 1/(2*n_tap) and a Gaussian distributed imaginary component with variance 1/(2*n_tap). The amplitude of each tap is thus Rayleigh distributed and the phase is Uniformly distributed. Since the power in each component is normalized by the filter length (n_tap) the BER performance would remain the same even if the filter length is changed (this has been verified experimentally).
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% FUNCTION TO SIMULATE PERFORMANCE OF 64-OFDM IN TIME VARYING FREQUENCY SELECTIVE CHANNEL
% n_bits: Input, length of binary sequence
% n_fft: Input, length of FFT (Fast Fourier Transform)
% EbNodB: Input, energy per bit to noise power spectral density ratio
% ber: Output, bit error rate
% Copyright RAYmaps (www.raymaps.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function[ber]= M_QAM_OFDM_fading(n_bits,n_fft,EbNodB)
Eb=7;
M=64;
k=log2(M);
n_cyc=32;
EbNo=10^(EbNodB/10);
x=transpose(round(rand(1,n_bits)));
h1=modem.qammod(M);
h1.inputtype='bit';
h1.symbolorder='gray';
y=modulate(h1,x);
n_sym=length(y)/n_fft;
n_tap=7;
for n=1:n_sym;
s_ofdm=sqrt(n_fft)*ifft(y((n-1)*n_fft+1:n*n_fft),n_fft);
s_ofdm_cyc=[s_ofdm(n_fft-n_cyc+1:n_fft); s_ofdm];
ht=(1/sqrt(2))*(1/sqrt(n_tap))*(randn(1,n_tap)+j*randn(1,n_tap));
Hf=fft(ht,n_fft);
r_ofdm_cyc=conv(s_ofdm_cyc,ht);
r_ofdm_cyc=(r_ofdm_cyc(1:n_fft+n_cyc));
wn=sqrt((n_fft+n_cyc)/n_fft)*(randn(1,n_fft+n_cyc)+j*randn(1,n_fft+n_cyc));
r_ofdm_cyc=r_ofdm_cyc+sqrt(Eb/(2*EbNo))*wn.';
r_ofdm=r_ofdm_cyc(n_cyc+1:n_fft+n_cyc);
s_est((n-1)*n_fft+1:n*n_fft)=(fft(r_ofdm,n_fft)/sqrt(n_fft))./Hf.';
end
h2=modem.qamdemod(M);
h2.outputtype='bit';
h2.symbolorder='gray';
h2.decisiontype='hard decision';
z=demodulate(h2,s_est.');
ber=(n_bits-sum(x==z))/n_bits
return
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
As before we have used an FFT size of 128 and cyclic prefix of 32 samples. The FFT and IIFT operations are normalized to maintain the signal to noise ratio (SNR). The extra energy transmitted in the cyclic prefix is also accounted for in the SNR calibration.
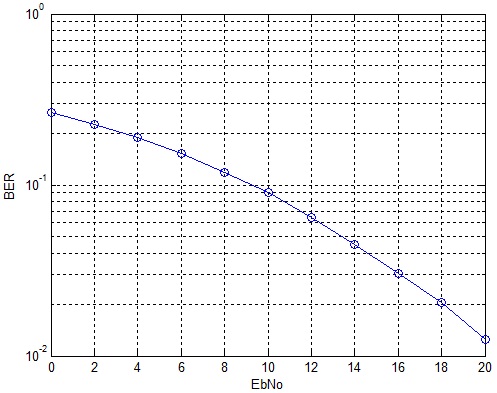
It is observed that the BER performance of 64-QAM OFDM in the time-varying frequency-selective channel is quite similar to that in the static frequency-selective channel with complex filter taps. It must be noted that with 64-QAM the goal is to achieve higher bit rate, error rates can be improved using antenna diversity and channel coding schemes.
Given below is the wrapper that should be used along with the above code. The wrapper basically calls the above routine for each value of EbNodB. The length of the binary sequence and the FFT size are other inputs to the function. The bit error rate at the specific EbNodB is the output of the function.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;
close all;
k=6;
n_fft=128;
l=k*n_fft*1e3;
EbNodB=0:2:20;
for n=1:length(EbNodB);n
ber(n)=M_QAM_OFDM_fading(l,n_fft,EbNodB(n));
end;
semilogy(EbNodB,ber,'O-');
grid on
xlabel('EbNo')
ylabel('BER')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
In future we would use the standard LTE channel models, namely EPA, EVA and ETU in our simulation.
Author: Yasir
More than 20 years of experience in various organizations in Pakistan, the USA, and Europe. Worked with the Mobile and Portable Radio Group (MPRG) of Virginia Tech and Qualcomm USA and was one of the first researchers to propose Space Time Block Codes for eight transmit antennas. Have publsihed a book “Recipes for Communication and Signal Processing” through Springer Nature.
19 thoughts on “BER of 64-QAM OFDM in Frequency Selective Fading-II”
Hello,
plz I need a matlab code showing a comparison between MQAM and QPSK (BER=f(Eb/N0))
Regards!
Sorry if this is a duplicate comment!
Thank you for the helpful tutorial.
You are using zero-forcing equalizer, right?
How can I implement this on a single-carrier system?
Also, if you could share some documents to help the code, that would be great 🙂
Many thanks in advance,
Fatima
Thank you for this helpful tutorial.
You are using zero-forcing equalizer, right?
How can I implement the code for a single-carrier system?
Can you attach some documents which you used to write the code?
Many thanks in advance,
Fatima
Hi, maybe I’m wrong… DMT systems need Hermitian symmetry before iFFT to get real numbers before cyclic prefix is added. Why is not done here?
Excellent tuorial
I’ve been digging up Google and found a function in Matlab can illustrate the theoretical BER for QAM which name is berfading
http://www.mathworks.com/help/toolbox/comm/ref/berfading.html
Thank you again for your fabulous post!
Thank you very much!
Just another question: What is the theoretical BER in this case (OFDM with MQAM in Reyleigh fading)? Can you plot it in the wrapper file, please?
I do not know of a theoretical formula for OFDM with MQAM in Rayleigh fading. If you find one please do post it here as well…
The Energy per Symbol for 16 QAM is calculated as:
Es=[(1+1)+(1+9)+(9+1)+(9+9)]/4=[40]/4=10
Since there are four bits per symbol:
Eb=10/4=2.5
Son: Use M=16 and calculate the Energy per Bit for this constellation and use it instead of Eb=7. I think this should do!
Thank you, sir. This is very helpful.
How can I modify this function code to compute BER for 16-QAM?
Jin: You will have to take a look at these posts.
http://www.raymaps.com/index.php/lte-fading-simulator/
http://www.raymaps.com/index.php/rayleigh-fading-simulator/
http://www.raymaps.com/index.php/highly-efficient-rayleigh-fading-simulator/
Bottom line is that you have to run the rayleigh fading simulator for each of the channel taps. You can use the Smith simulator or the more efficient Young simulator to generate the temporally correlated fading sequences.
For M_QAM_OFDM_fading, temporal correlation is not considered. However, I wish to consider the temporal correlarion over simulation of BER of 64-QAM OFDM in Frequency S elective Fading-II. I red your LTE simulator, but I want to your help because of my poor knowledge. How do I revise the Matlab code?
For Frequency Selective Fading-II the matlab code, M_QAM_OFDM_fading, the channel is time-varying frequency selective but does not have temporal correlation. Considering the temporal correlation in M_QAM_OFDM_fading, what is the revision in the code?
Thanks, the code has executed just made a small execution mistake.
Save the function as “M_QAM_OFDM_fading.m” and the wrapper with any name you want. Let me know if you still get an error.
For BER of 64-QAM OFDM in Frequency Selective Fading-II the matlab code has been showing an error as “EbNodB is undefined” and with what name should the wrapper file be saved?
Please save the wrapper file as *.m file in the same folder as the above function.